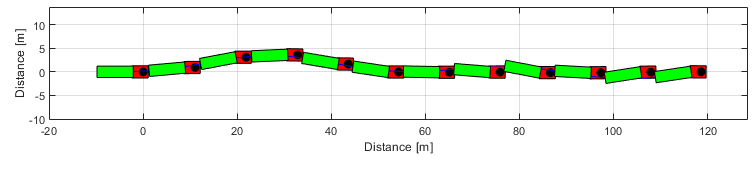
Multi-axle steering articulated

This script presents open-loop multi-axle steering of an articulated vehicle.

Simulation models and parameters
Simulation parameters
Open-loop steering input
Run simulation
Results
See Also

Simulation models and parameters

First, all classes of the package are imported with

clear ; close all ; clc

import VehicleDynamicsLateral.*

Choosing tire and vehicle model. In this case, the parameters are defined by the user.

% Choosing tire
TireModel = TirePacejka();
TireModel.a0        = 1;
TireModel.a1        = 2;
TireModel.a2        = 700;
TireModel.a3        = 5000;
TireModel.a4        = 80;
TireModel.a5        = 0;
TireModel.a6        = 0;
TireModel.a7        = 0.6;

% Choosing vehicle
VehicleModel = VehicleArticulatedNonlinear();
VehicleModel.mF0    = 5200;
VehicleModel.mR0    = 2400;
VehicleModel.mF     = 6000;
VehicleModel.mR     = 10000;
VehicleModel.mM     = 17000;
VehicleModel.IT     = 46000;
VehicleModel.IS     = 450000;
VehicleModel.lT     = 3.5;
VehicleModel.lS     = 7.7;
VehicleModel.c      = -0.3;
VehicleModel.nF     = 2;
VehicleModel.nR     = 4;
VehicleModel.nM     = 8;
VehicleModel.wT     = 2.6;
VehicleModel.wS     = 2.4;
VehicleModel.muy    = 0.8;
VehicleModel.deltaf = 0;
VehicleModel.deltar = 0;
VehicleModel.deltam = 0;
VehicleModel.Fxf    = 0;
VehicleModel.Fxr    = 0;
VehicleModel.Fxm    = 0;

% The System is completely defined once we atribute the chosen tire model
% to the vehicle object.

VehicleModel.tire = TireModel;

Simulation parameters

Choosing simulation time span

T       = 11;                           % Total simulation time     [s]
resol   = 80;                           % Resolution
TSPAN   = 0:T/resol:T;                  % Time span                 [s]

Open-loop steering input

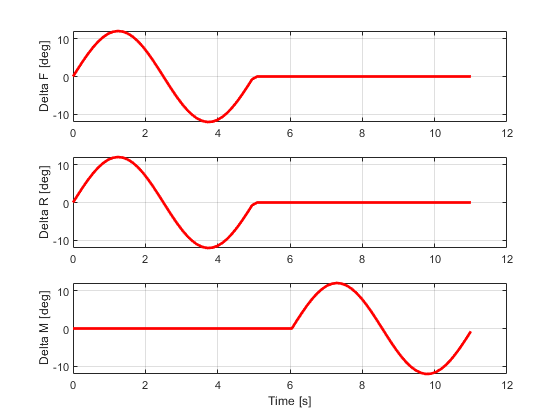
Single period sine wave with:

delta_amplitude     = 12*pi/180;        % Steering input amplitude  [rad]
T_period            = 5;                % Steering single period    [s]
freq                = 1/T_period;       % Steering frequency        [Hz]
delta_freq          = freq*2*pi;        % Steering frequency        [rad/s]

% End input index
sine_index          = find(TSPAN > T_period);

% Defining steering input
VehicleModel.deltaf = [delta_amplitude*sin(delta_freq*TSPAN(1:sine_index(1)-1)) zeros(1,length(TSPAN)-sine_index(1)+1)];
VehicleModel.deltar = [delta_amplitude*sin(delta_freq*TSPAN(1:sine_index(1)-1)) zeros(1,length(TSPAN)-sine_index(1)+1)];
VehicleModel.deltam = [zeros(1,length(TSPAN)-sine_index(1)+1) delta_amplitude*sin(delta_freq*TSPAN(1:sine_index(1)-1))];

figure
subplot(3,1,1)
    hold on ; grid on ; box on
    plot(TSPAN,VehicleModel.deltaf*180/pi,'r','linewidth',2)
    ylabel('Delta F [deg]')
subplot(3,1,2)
    hold on ; grid on ; box on
    plot(TSPAN,VehicleModel.deltar*180/pi,'r','linewidth',2)
    ylabel('Delta R [deg]')
subplot(3,1,3)
    hold on ; grid on ; box on
    plot(TSPAN,VehicleModel.deltam*180/pi,'r','linewidth',2)
    ylabel('Delta M [deg]')
    xlabel('Time [s]')

To define a simulation object (simulator) the arguments must be the vehicle object and the time span.

simulator = Simulator(VehicleModel, TSPAN);

Initial conditions Changing initial conditions of the simulation object

simulator.V0 = 40/3.6;              % Initial velocity              [m/s]

Run simulation

To simulate the system we run the Simulate method of the simulation object.

simulator.Simulate();

Results

g = Graphics(simulator);
g.TractorColor = 'r';
g.SemitrailerColor = 'g';
g.Frame();
g.Animation();
% g.Animation('html/MultiaxleSteeringArticulated');       % Uncomment to save animation gif