Tire models

The tire models describe the forces in the road-tire interactions according to the dynamic condition of the vehicle.

The typical relation between the lateral force and the slip angle can be observed in Fig. 61. Besides, it is possible to verify the definition of slip angle.

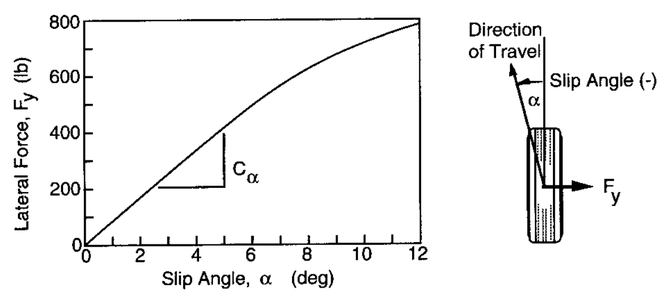
Fig. 61 Tire lateral force and slip angle (Adapted from [Gil92]).

Linear

The linear tire model describes a linear relationship between tire lateral force and slip angle.

The lateral force of the tire can be calculated as

\[F_y = K \alpha\]

where \(F_y\) is the lateral force, \(K\) is the cornering stiffness and \(\alpha\) is the tire slip angle.

This model is only valid for small values of slip angle

Pacejka (Magic Formula)

Nonlinear relationship between tire lateral force and slip angle expressed by a semi-empirical model with experimental coefficients [BPL89].

The lateral force can be written as

\[F_y = - \frac{\mu_y}{\mu_{y, n}} \left( F_{y, n} \left(\alpha_{eq} \right) + S_v \right)\]

where \(\alpha_{eq}\) is the equivalent slip angle

\[\alpha_{eq} = \frac{\mu_{y0}}{\mu_y} \frac{F_{z0}}{F_z} \left( \alpha + S_h \right)\]

and \(F_{y, n}\) is the reference function of the lateral force

\[F_{y, n} = D \sin\left(C \arctan\left(B \alpha - E \left(B \alpha - \arctan\left(B \alpha\right)\right)\right)\right)\]

The coefficients \(B\), \(C\), \(D\) and \(E\) can be written as

\[\begin{split}C &= a_0 \\ D &= \mu_{y, n} F_z = (a_1 F_z + a_2) F_z \\ B &= \frac{B C D}{C D} = a_3 \sin \left\{ 2 \arctan \left( \frac{F_z}{a_4} \right) \right\} (1 - a_5 | \gamma |) \\ E &= a_6 F_z + a_7\end{split}\]

The horizontal and vertical shifts of the curve are calculated as

\[\begin{split}S_h &= a_8 \gamma + a_9 F_z + a_{10} \\ S_v &= a_{11} F_z \gamma + a_{12} F_z + a_{13}\end{split}\]

The model implemented here converts the slip angle using the following equation

_ALPHA = asin(sin(alpha));_

This equation alters the slip angle in such way that the characteristic equation becames symmetric in relation to the vertical line at 90 degrees and the lateral force becomes zero at 180 degrees. The same analogy can be made with negative values of the slip angle. Thus, this model covers the whole range of slip angles (-180 to 180 degrees).

Polynomial

Nonlinear relation between tire lateral force and slip angle expressed by a third order polinomial equation.

This model is used by several authors [JH84][SW13][SH98].

The equation of the model is given by

\[F_y = k_1 \alpha - k_2\alpha^3\]

where \(F_y\) is the lateral force and \(\alpha\) is the tire slip angle. \(k_1\) and \(k_2\) are the model coefficients. This model is valid up to the maximal lateral force (Tire saturation).

Tire comparison

Under construction.