Sinusoidal Steering

Simulation of a simple vehicle with sinusoidal steering actuation.

First, we choose the tire and vehicle models.

TireModel = TirePacejka();          % Choosing tire
System = VehicleSimpleNonlinear();  % Choosing vehicle

The system is completely defined once we attribute the chosen tire model to the vehicle object.

System.tire = TireModel;

The friction coefficient between the tire and the road can be set as

System.muy = 1.0;

After this, we define the simulation time span

T = 4;                              % Total simulation time [s]
resol = 50;                         % Resolution
TSPAN = 0:T/resol:T;                % Time span [s]

We want to simulate the model with an open loop sinusoidal steering input. So, since we have the time span, we can create an array with the value of the steering angle for each simulated instants.

System.deltaf = 1*pi/180*sin(T^-1*2*pi*TSPAN);

The steering input over time can be plotted with

f1 = figure(1);
grid on ; box on;
plot(TSPAN,180/pi*System.deltaf)
xlabel('time [s]')
ylabel('Steering angle [deg]')

The resulting plot is illustrated below

Fig. 21 Open loop steering angle over time

To define a simulation object (Simulator) the arguments must be the vehicle object and the time span. This is,

simulator = Simulator(System, TSPAN);

No simulation parameters need to be altered. So, we have everything needed to run the simulation. For this, we use

simulator.Simulate();

The resulting time response of each state is stored in separate variables:

XT = simulator.XT;
YT = simulator.YT;
PSI = simulator.PSI;
VEL = simulator.VEL;
ALPHAT = simulator.ALPHAT;
dPSI = simulator.dPSI;

Frame and animation can be generated defining a graphic object (Graphics). The only argument of the graphic object is the simulator object after the simulation.

g = Graphics(simulator);

To change the color of the vehicle run

g.TractorColor = 'r';

To generate the frame/animation with a different horizontal and vertical scale run

g.Frame('scalefig',3);
g.Animation('scalefig',3);

Both graphics feature can be seen below.

Fig. 22 Frame of the articulated vehicle model.

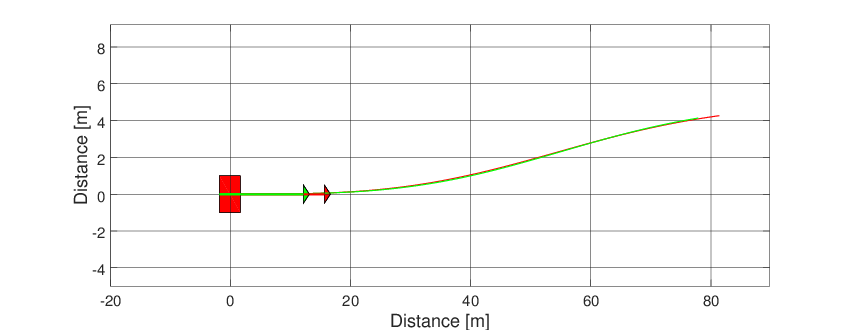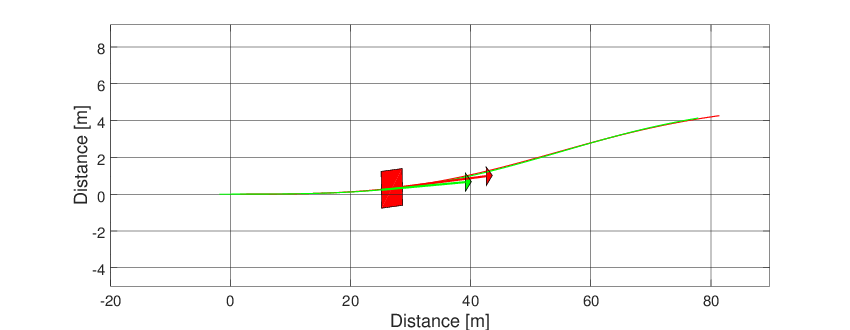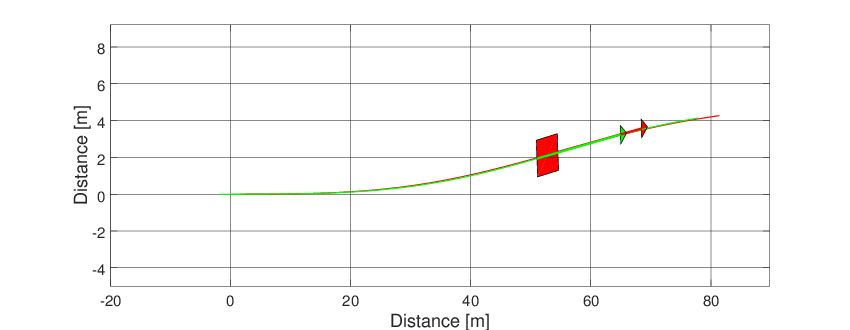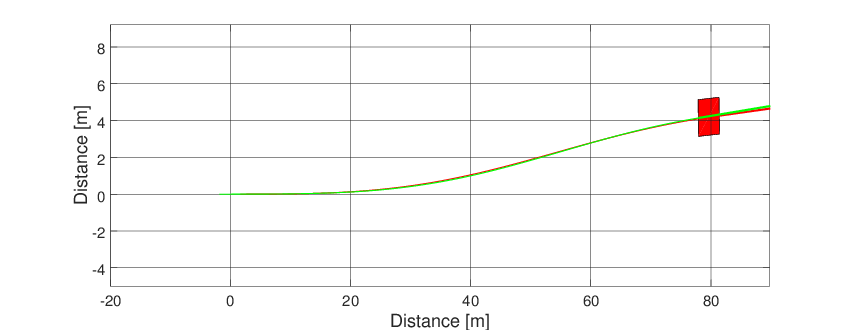
Fig. 23 Animation of the articulated vehicle model.