SkidPad

This example shows the maneuver of a nonlinear simple vehicle with Pacejka tire model moving in circles.

The main script is described in SkidPad.m. A control law (rear-wheel-drive) is used to maintain a constant CG speed. The control is implemented in the VelControl.m file.

SkidPad.m

First, we choose the tire and vehicle models. The first one is the Pacejka tire model (Pacejka (Magic Formula)) and the second one is the nonlinear vehicle model (Simple vehicle 3 DOF).

TireModel = TirePacejka();          % Choosing tire
System = VehicleSimpleNonlinear();  % Choosing vehicle

The default parameters of the vehicle and tire model can be seen in VehicleSimpleNonlinear and TirePacejka, respectively.

Changing the vehicle parameters

System.mF0 = 700;
System.mR0 = 600;
System.IT = 10000;
System.lT = 3.5;
System.nF = 2;
System.nR = 2;
System.wT = 2;
System.muy = .8;

Check all the vehicle parameters at VehicleSimpleNonlinear.

The input variables can be defined as

System.deltaf = 20*pi/180;
System.Fxf = 0;
System.Fxr = @VelControl;

When the input variables are defined as a scalar quantity, the attributed value remains the same for the entire simulation span. However, we can see that the longitudinal force of the rear axle recieves the handle of the VelControl.m function.

The System is completely defined once we attribute the chosen tire model to the vehicle object.

System.tire = TireModel;

Choosing the simulation time span

T = 10;                             % Total simulation time [s]
resol = 100;                        % Resolution
TSPAN = 0:T/resol:T;                % Time span [s]

To define a simulation object (Simulator) the arguments must be the vehicle object and the time span.

simulator = Simulator(System, TSPAN);

The initial velocity of the center of gravity can be changed running

simulator.V0 = 8.333;

Now, we have everything needed to run the simulation. For this, we use

simulator.Simulate();

The resulting time response of each state is stored in separate variables:

XT = simulator.XT;
YT = simulator.YT;
PSI = simulator.PSI;
VEL = simulator.VEL;
ALPHAT = simulator.ALPHAT;
dPSI = simulator.dPSI;

The following lines plot the time response of each state of the model.

f1 = figure(1);
hold on ; grid on ; box on
plot(TSPAN,XT)
xlabel('time [s]')
ylabel('Distance in the x direction [m]')

f2 = figure(2);
hold on ; grid on ; box on
plot(TSPAN,YT)
xlabel('time [s]')
ylabel('Distance in the y direction [m]')

f3 = figure(3);
hold on ; grid on ; box on
plot(TSPAN,PSI)
xlabel('time [s]')
ylabel('Yaw angle [rad]')

f4 = figure(4);
hold on ; grid on ; box on
plot(TSPAN,VEL)
xlabel('time [s]')
ylabel('Velocity [m/s]')

f5 = figure(5);
hold on ; grid on ; box on
plot(TSPAN,ALPHAT)
xlabel('time [s]')
ylabel('Vehicle slip angle [rad/s]')

f6 = figure(6);
hold on ; grid on ; box on
plot(TSPAN,dPSI)
xlabel('time [s]')
ylabel('Yaw rate [rad/s]')

The generated figures can be seen below.

Fig. 24 Longitudinal position of the center of gravity of the system.

Fig. 25 Transversal position of the center of gravity of the system.

Fig. 26 Yaw angle of the vehicle

Fig. 27 Velocity of the center of gravity

Fig. 28 Vehicle slip angle

Fig. 29 Vehicle yaw rate

Frame and animation can be generated defining a graphic object (Graphics). The only argument of the graphic object is the simulator object after the simulation.

g = Graphics(simulator);

To change the color of the vehicle run

g.TractorColor = 'c';

The frame can be generated running

g.Frame();

We can fit a circle to verify the trajectory of the center of gravity. This is done using the function circfit.m

angulo = 0:0.01:2*pi;

[R,XC,YC] = circfit(XT(40:end),YT(40:end));

XX = XC + R*cos(angulo);
YY = YC + R*sin(angulo);

hold on
plot(XX,YY,'k')

The animation can be generated running

g.Animation();

Both graphics feature can be seen below.

Fig. 30 Frame of the simple vehicle model.

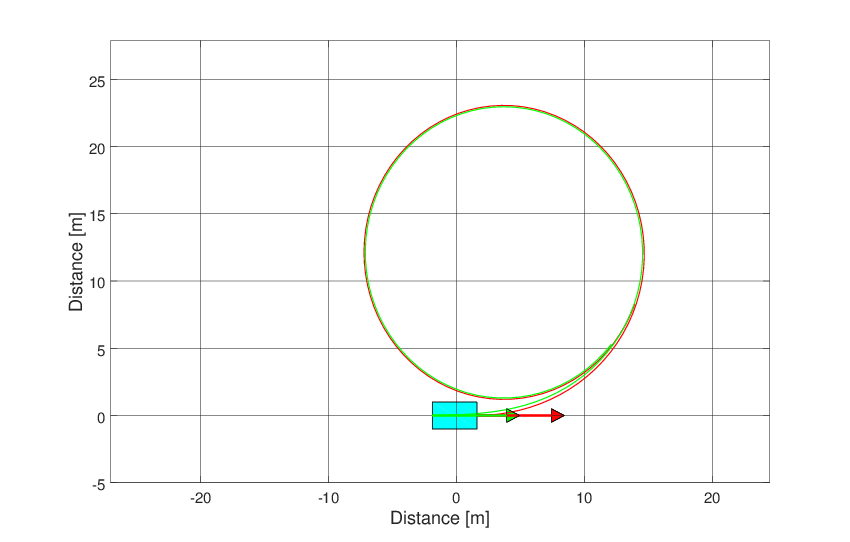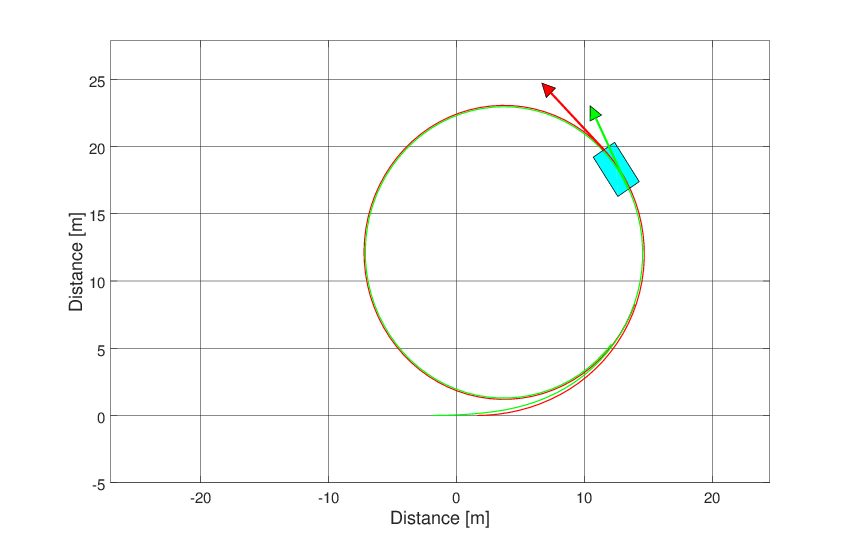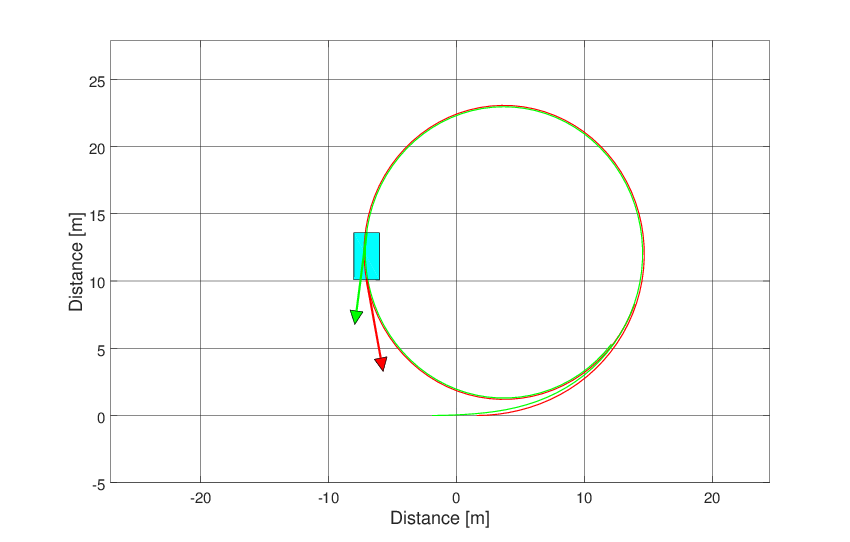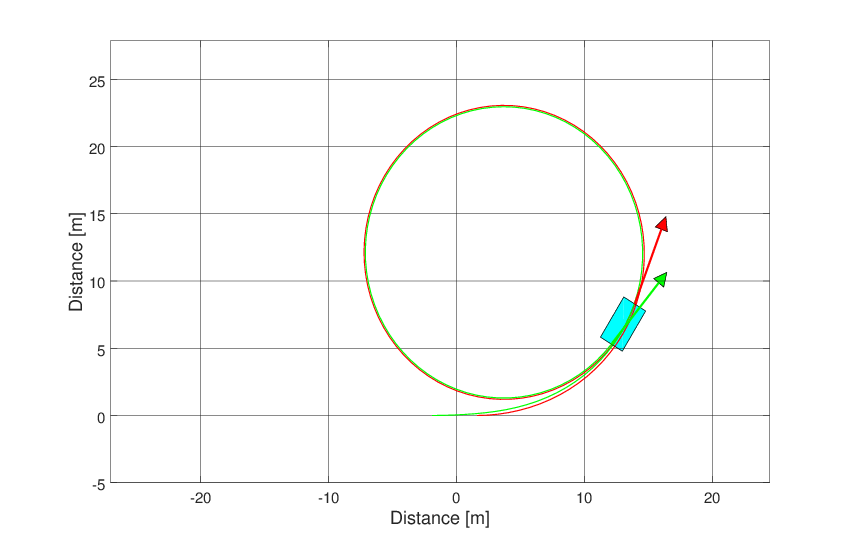
Fig. 31 Animation of the simple vehicle model.

VelControl.m

The control law of the longitudinal system is depicted below.

function output = VelControl(input,~)
    % Current velocity
    vel = input(4);
    % Reference velocity
    velRef = 8.333;

    % Control gain
    K = 100000;

    output = K * (velRef - vel);

circfit.m

The function used do fit a circle is depicted below.

function [r,varargout]=circfit(x,y)
%CIRCFIT  Least squares fit of X-Y data to a circle.
%   R = CIRCFIT(X,Y) returns scalar radius R of a fitted circle. X and Y are 1-D
%   arrays of position data in a rectilinear coordinate system. X and Y must be
%   the same length and must contain at least three non-colinear points in order
%   for a valid solution to be found.
%
%   [R,ERR] = CIRCFIT(X,Y) additionally returns the scalar root mean squared
%   error of the fitted circle radius and center relative to the position data.
%
%   [R,XC,YC] = CIRCFIT(X,Y) additionally returns the scalar positions, XC and
%   YC, of center of the fitted circle.
%
%   [R,XC,YC,ERR] = CIRCFIT(X,Y) returns both the center positions of the circle
%   as well as the root mean squared error.
%
%   examples:
%       % Fit of just five noisy points
%       x1=[1 0 -1 0 1]+0.05*randn(1,5); y1=[0 1 0 -1 0]+0.05*randn(1,5);
%       r1=circfit(x1,y1)
%
%       % CIRCFIT can sometimes perfom poorly with less than 180-degree arc
%       t=0:0.1:pi; lt=length(t);
%       x2=cos(t)+0.04*randn(1,lt); y2=sin(t)+0.04*randn(1,lt);
%       r2_90deg=circfit(x2(1:floor(lt/2)),y2(1:floor(lt/2)))
%       r2_180deg=circfit(x2,y2)

%   Andrew D. Horchler, adh9 @ case . edu, Created 5-12-7
%   Revision: 1.3, 4-6-16


% Check inputs
if nargout > 4
    error('circfit:circfit:TooManyOutputs','Too many output arguments.');
end

if ~isvector(x) || ~isfloat(x) || ~isreal(x) || ~all(isfinite(x))
    error('circfit:circfit:NonFiniteRealVectorX',...
          'X must be a finite real vector of floating point numbers.');
end
if ~isvector(y) || ~isfloat(y) || ~isreal(y) || ~all(isfinite(y))
    error('circfit:circfit:NonFiniteRealVectory',...
          'Y must be a finite real vector of floating point numbers.');
end

lx=length(x);
if lx ~= length(y)
    error('circfit:circfit:LengthMismatch',...
          'The vectors X and Y must have the same length.');
end
if lx < 3
    error('circfit:circfit:Min3Points',...
          'The vectors X and Y must contain at least three points.');
end
x=x(:);
y=y(:);

% Check collinearity, assume with sufficient points, some will be non-collinear
if rank(diff([x([1:min(50,lx) 1]) y([1:min(50,lx) 1])])) == 1
    if lx <= 50 || rank(diff([x y;x(1) y(1)])) == 1
        error('circfit:circfit:Colinearity',...
             ['The points in vectors X and Y must not all be collinear, or '...
              'nearly collinear, with each other.']);
    end
end

xx=x.*x;
yy=y.*y;
xy=x.*y;
xxyy=xx+yy;
sx=sum(x);
sy=sum(y);
sxx=sum(xx);
syy=sum(yy);
sxy=sum(xy);

% Solve linear system without inverting
% a=[sx sy lx;sxy syy sy;sxx sxy sx]\[sxx+syy;sum(xxyy.*y);sum(xxyy.*x)];
[L,U]=lu([sx sy lx;sxy syy sy;sxx sxy sx]);
a=U\(L\[sxx+syy;sum(xxyy.*y);sum(xxyy.*x)]);

xc=0.5*a(1);          	% X-position of center of fitted circle
yc=0.5*a(2);          	% Y-position of center of fitted circle
r=sqrt(xc^2+yc^2+a(3));	% Radius of fitted circle

% Set variable outputs
if nargout > 2
    varargout{1}=xc;
    varargout{2}=yc;
end
if nargout == 2 || nargout == 4
    varargout{nargout-1}=sqrt(mean((sqrt((x-xc).^2+(y-yc).^2)-r).^2));	% RMSE
end