Template Articulated Simulink

This template shows how to simulate an articulated vehicle in Simulink using a s-function. The graphics are also plotted.

This model uses the s-function ArticulatedVehicleSFunction.m in Simulink. The package and this s-function must be in Matlab path.

The “ArticulatedVehicleSimulink.slx” available in the repository (“examples/TemplateArticulatedSimulink”) is illustrated below:

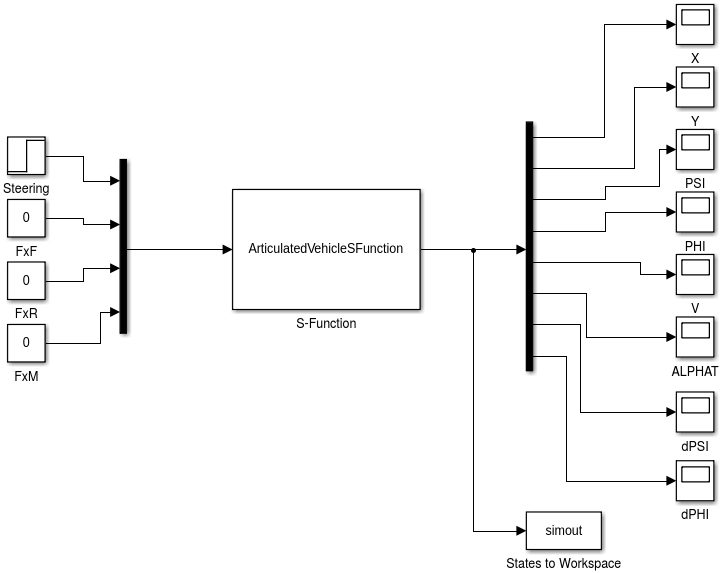
Fig. 49 Articulated vehicle simulink S-Function

It can be seen that the longitudinal forces of the tire are zero for the entire simulation. The steering angle recieve a step input.

Template

To simulate the model run

sim('ArticulatedVehicleSimulink');

Each vehicle state variable goes to a scope. And the output of the model is saved in the workspace.

To generate the graphics, the same model used in Articulated Vehicle S-Function must be defined.

Todo

Improve generation of graphics. Define parameters once -> Run Simulink -> Retrieve responses -> Graphics

First, define the tire model.

TireModel = TirePacejka();          % Choosing tire model

Defining the tire parameters to match the parameters used in the S-Function.

TireModel.a0 = 1;
TireModel.a1 = 2;
TireModel.a2 = 700;
TireModel.a3 = 5000;
TireModel.a4 = 80;
TireModel.a5 = 0;
TireModel.a6 = 0;
TireModel.a7 = 0.6;
TireModel.a8 = 0;
TireModel.a9 = 0;
TireModel.a10 = 0;
TireModel.a11 = 0;
TireModel.a12 = 0;
TireModel.a13 = 0;

The vehicle model is defined as

VehicleModel = VehicleArticulatedNonlinear();

Defining the vehicle parameters to match the parameters used in the S-Function.

VehicleModel.mF0 = 5200;
VehicleModel.mR0 = 2400;
VehicleModel.mF = 6000;
VehicleModel.mR = 10000;
VehicleModel.mM = 17000;
VehicleModel.IT = 46000;
VehicleModel.IS = 450000;
VehicleModel.lT = 3.5;
VehicleModel.lS = 7.7;
VehicleModel.c = -0.3;
VehicleModel.nF = 2;
VehicleModel.nR = 4;
VehicleModel.nM = 8;
VehicleModel.wT = 2.6;
VehicleModel.wS = 2.4;
VehicleModel.muy = 0.8;
VehicleModel.deltaf = 0;
VehicleModel.Fxf = 0;
VehicleModel.Fxr = 0;
VehicleModel.Fxm = 0;
VehicleModel.tire = TireModel;

Defining the simulation object.

simulator = Simulator(VehicleModel, tout);

Retrieving state responses from Simulink model

simulator.XT = simout.Data(:,1);
simulator.YT = simout.Data(:,2);
simulator.PSI = simout.Data(:,3);
simulator.PHI = simout.Data(:,4);
simulator.VEL = simout.Data(:,5);
simulator.ALPHAT = simout.Data(:,6);
simulator.dPSI = simout.Data(:,7);
simulator.dPHI = simout.Data(:,8);

Frame and animation can be generated defining a graphic object (Graphics). The only argument of the graphic object is the simulator object after the simulation.

g = Graphics(simulator);

To change the color of the tractor and the semitrailer run

g.TractorColor = 'r';
g.SemitrailerColor = 'g';

After that, just run

g.Frame();
g.Animation();

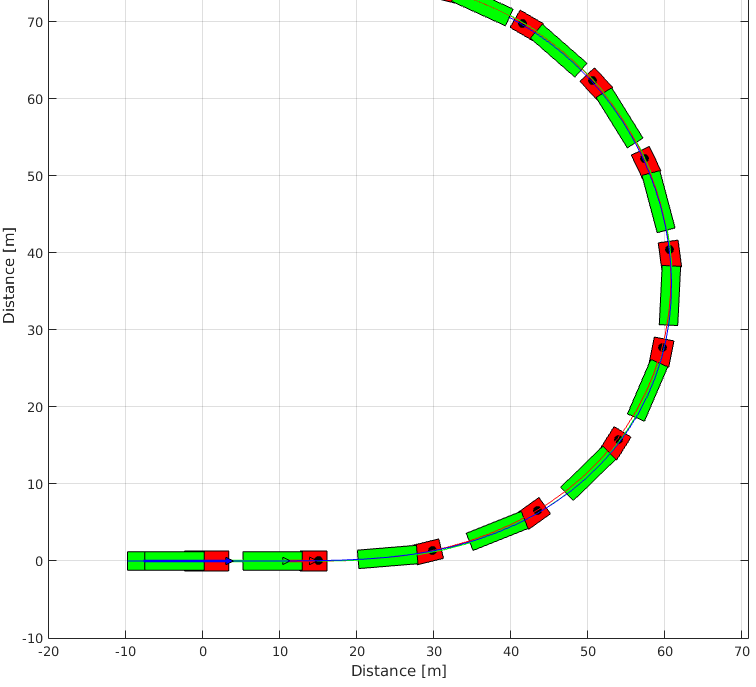
Both graphics feature can be seen below.

Fig. 50 Frame of the simple vehicle model in Simulink.

Todo

Include Template Simple Simulink Animation

As expected the vehicle starts traveling in a straight line and starts a turn at (t = 1 , s) because of the step function.

Articulated Vehicle S-Function

The articulated vehicle S-Function is depicted below.

function [sys,x0,str,ts] = ArticulatedVehicleSFunction(t,x,u,flag)
% This file is a s-function template for simulating the articulated vehicle model in Simulink.

% Choosing tire model
TireModel = TirePacejka();
% Defining tire parameters
TireModel.a0 = 1;
TireModel.a1 = 2;
TireModel.a2 = 700;
TireModel.a3 = 5000;
TireModel.a4 = 80;
TireModel.a5 = 0;
TireModel.a6 = 0;
TireModel.a7 = 0.6;
TireModel.a8 = 0;
TireModel.a9 = 0;
TireModel.a10 = 0;
TireModel.a11 = 0;
TireModel.a12 = 0;
TireModel.a13 = 0;

% Choosing vehicle model
VehicleModel = VehicleArticulatedNonlinear();
% Defining vehicle parameters
VehicleModel.mF0 = 5200;
VehicleModel.mR0 = 2400;
VehicleModel.mF = 6000;
VehicleModel.mR = 10000;
VehicleModel.mM = 17000;
VehicleModel.IT = 46000;
VehicleModel.IS = 450000;
VehicleModel.lT = 3.5;
VehicleModel.lS = 7.7;
VehicleModel.c = -0.3;
VehicleModel.nF = 2;
VehicleModel.nR = 4;
VehicleModel.nM = 8;
VehicleModel.wT = 2.6;
VehicleModel.wS = 2.4;
VehicleModel.muy = 0.8;
VehicleModel.deltaf = 0;
VehicleModel.Fxf = 0;
VehicleModel.Fxr = 0;
VehicleModel.Fxm = 0;
VehicleModel.tire = TireModel;

switch flag,

  %%%%%%%%%%%%%%%%%%
  % Initialization %
  %%%%%%%%%%%%%%%%%%
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes();

  %%%%%%%%%%%%%%%
  % Derivatives %
  %%%%%%%%%%%%%%%
  case 1,
    sys=mdlDerivatives(t,x,u,VehicleModel);

  %%%%%%%%%%%
  % Outputs %
  %%%%%%%%%%%
  case 3,
    sys=mdlOutputs(t,x,u,VehicleModel);

  %%%%%%%%%%%%%%%%%%%
  % Unhandled flags %
  %%%%%%%%%%%%%%%%%%%
  case { 2, 4, 9 },
    sys = [];

  %%%%%%%%%%%%%%%%%%%%
  % Unexpected flags %
  %%%%%%%%%%%%%%%%%%%%
  otherwise
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));

end
% end csfunc

%
%=============================================================================
% mdlInitializeSizes
% Return the sizes, initial conditions, and sample times for the S-function.
%=============================================================================
%
function [sys,x0,str,ts]=mdlInitializeSizes()

% Definitions
sizes = simsizes;
sizes.NumContStates  = 8;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 8;
sizes.NumInputs      = 4;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;

sys = simsizes(sizes);

% Setting initial conditions
x0  = [0 0 0 0 15 0 0 0];
str = [];
ts  = [0 0];

% end mdlInitializeSizes
%
%=============================================================================
% mdlDerivatives
% Return the derivatives for the continuous states.
%=============================================================================
%


function sys = mdlDerivatives(t,x,u,vehicle)

% Defining input
vehicle.deltaf = u(1);
vehicle.Fxf = u(2);
vehicle.Fxr = u(3);
vehicle.Fxm = u(4);

% Getting the vehicle model function (state equations)
ModelFunction = @vehicle.Model;
% Getting the mass matrix function of the model
MassMatrixFunction = @vehicle.MassMatrix;

% The derivatives are calculated with the inverse of the MassMatrix
sys = MassMatrixFunction(t,x)\ModelFunction(t,x,0);

% end mdlDerivatives
%
%=============================================================================
% mdlOutputs
% Return the block outputs.
%=============================================================================
%
function sys=mdlOutputs(~,x,~,~)

% Output are all state variables
sys = x;

% end mdlOutputs