Steering Control

LQR steering control of autonomous vehicles in obstacle avoidance maneuvers.

This example requires the control package.

SteeringControl.m

First, we choose the tire model

TirePac = TirePacejka();

and define the tire parameters

Fz = 4e+03;
camber = 0;
TirePac.a0 = 1;
TirePac.a1 = 0;
TirePac.a2 = 800;
TirePac.a3 = 10000;
TirePac.a4 = 50;
TirePac.a5 = 0;
TirePac.a6 = 0;
TirePac.a7 = -1;
TirePac.a8 = 0;
TirePac.a9 = 0;
TirePac.a10 = 0;
TirePac.a11 = 0;
TirePac.a12 = 0;
TirePac.a13 = 0;

The plant model is defined with

VehiclePlant = VehicleSimpleNonlinear();

The vehicle parameters are

VehiclePlant.mF0 = 700;
VehiclePlant.mR0 = 600;
VehiclePlant.IT = 10000;
VehiclePlant.lT = 3.5;
VehiclePlant.nF = 1;
VehiclePlant.nR = 1;
VehiclePlant.wT = 1.8;
VehiclePlant.muy = 1;

Attributing the chosen tire model to the vehicle object we have

VehiclePlant.tire = TirePac;

The input steering angle is given by the control law within the ControlLaw.m function.

VehiclePlant.deltaf = @ControlLaw;

After this, we define the simulation time span

T = 12;                             % Total simulation time [s]
resol = 500;                        % Resolution
TSPAN = 0:T/resol:T;                % Time span [s]

To define a simulation object (Simulator) the arguments must be the vehicle object and the time span. This is,

simulator = Simulator(VehiclePlant, TSPAN);

The default parameters of the simulation object can be found in Simulator. However, we are interested in changing the initial velocity of the vehicle. This can be done running

simulator.V0 = 16.7;

Now, we have everything needed to run the simulation. For this, we use

simulator.Simulate();

The resulting time response of each state is stored in separate variables:

XT = simulator.XT;
YT = simulator.YT;
PSI = simulator.PSI;
VEL = simulator.VEL;
ALPHAT = simulator.ALPHAT;
dPSI = simulator.dPSI;

x = [XT YT PSI VEL ALPHAT dPSI]; % ??

Preallocating the control input array

u = zeros(length(TSPAN),1); % ??
controlEffort = zeros(length(TSPAN),1);

Retrieving the control input of the system based on the simulation results

for ii = 1:length(TSPAN)
    controlEffort(ii) = ControlLaw(x(ii,:));
end

The steering input can be plotted with

f1 = figure(1);
hold on; box on; grid on
plot(TSPAN,controlEffort*180/pi,'k')
xlabel('Time [s]');
ylabel('Steering input [deg]');

The resulting control input is

Fig. 44 Control input of the vehicle.

Frame and animation can be generated defining a graphic object (Graphics). The only argument of the graphic object is the simulator object after the simulation.

g = Graphics(simulator);

To generate the frame/animation with a different horizontal and vertical scale run

g.Frame('scalefig',3);

The track limits can be added to the plot with the following code

carWidth = 2;
LaneOffset = 3.5;

section1width = 1.1*carWidth + 0.25;
section3width = 1.2*carWidth + 0.25;
section5width = 1.3*carWidth + 0.25;

section1Inf = -section1width/2;
section1Sup = section1width/2;

section3Inf = section1Inf+LaneOffset;
section3Sup = section3Inf+section3width;
section3Center = (section3Inf+section3Sup)/2;

section5Inf = -section5width/2;
section5Sup = section5width/2;

plot([0 15],[section1Inf section1Inf],'k')          % linha inferior
plot([0 15],[section1Sup section1Sup],'k')          % linha superior
plot([0 15],[0 0],'k--')                            % linha central

plot([15 45],[0 section3Center],'k--')              % linha central

plot([45 70],[section3Inf section3Inf],'k')         % linha inferior
plot([45 70],[section3Sup section3Sup],'k')         % linha superior
plot([45 70],[section3Center section3Center],'k--') % linha central

plot([70 95],[section3Center 0],'k--')

plot([95 130],[section5Inf section5Inf],'k')
plot([95 130],[section5Sup section5Sup],'k')
plot([95 130],[0 0],'k--')

The resulting frame can be seen below.

Fig. 45 Frame of the steering control example.

The animation is generated with

g.Animation(‘scalefig’,3);

The resulting animation can be seen below.

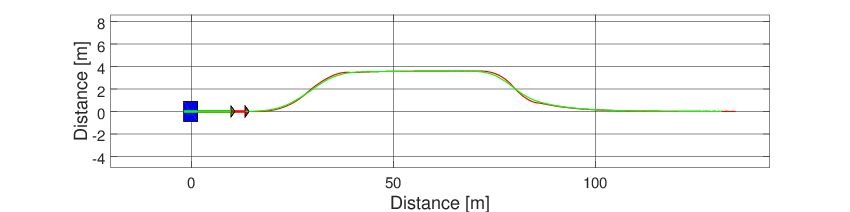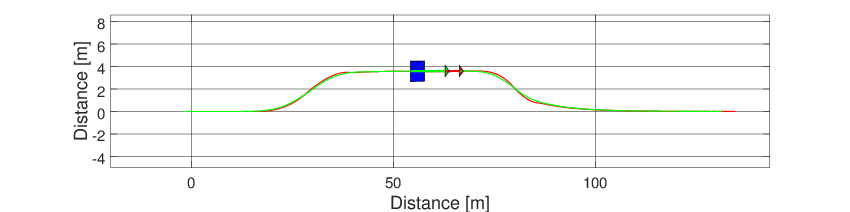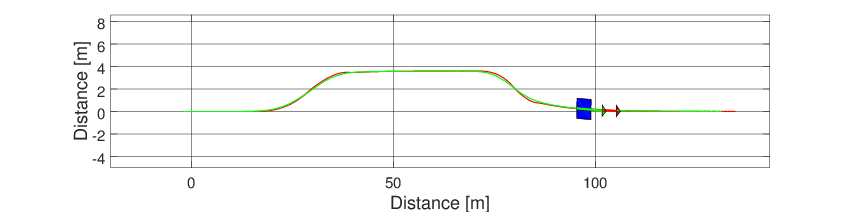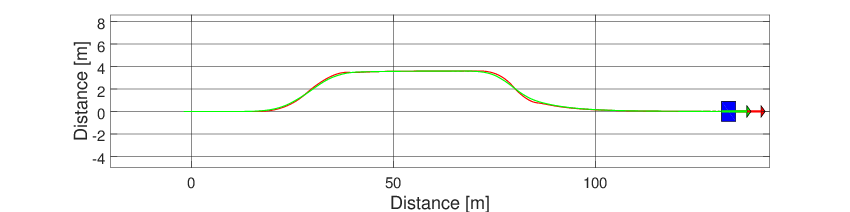
Fig. 46 Frame of the steering control example.

ControlLaw.m

The vehicle model used in the control design is based on the Simple vehicle 4 DOF.

The state vector is given by

\[\begin{split}{\bf x} = \left[ \begin{array}{c} {\rm x}_1 \\ {\rm x}_2 \\ {\rm x}_3 \\ {\rm x}_4 \\ {\rm x}_5 \\ {\rm x}_6 \end{array} \right] = \left[ \begin{array}{c} x \\ y \\ \psi \\ v_{\rm T} \\ \alpha_{\rm T} \\ \dot{\psi} \end{array} \right]\end{split}\]

The state equation is

\[\begin{split}\dot{{\rm x}}_1 &= {\rm x}_4 \cos \left( {\rm x}_3 + {\rm x}_5 \right) \\ \dot{{\rm x}}_2 &= {\rm x}_4 \sin \left( {\rm x}_3 + {\rm x}_5 \right) \\ \dot{{\rm x}}_3 &= {\rm x}_6 \\ \dot{{\rm x}}_4 &= \frac{F_{y,{\rm F}} \sin \left( {\rm x}_5 - \delta \right) + F_{y,{\rm R}} \sin {\rm x}_5}{m_{T}} \\ \dot{{\rm x}}_5 &= \frac{F_{y,{\rm F}} \cos \left( {\rm x}_5 - \delta \right) + F_{y,{\rm R}} \cos \alpha_{\rm T} - m_{T} {\rm }_4 {\rm x}_6}{m_{T} {\rm x}_4} \\ \dot{{\rm x}}_6 &= \frac{F_{y,{\rm F}} a \cos \delta - F_{y,{\rm R}} b}{I_{T}} \\\end{split}\]

and the slip angles are

\[\begin{split}\alpha_{\rm F} &= \arctan \left( \frac{v_{\rm T} \sin \alpha_{\rm T} + a \dot{\psi}}{ v_{\rm T} \cos \alpha_{\rm T}} \right) - \delta \\ \alpha_{\rm R} &= \arctan \left( \frac{v_{\rm T} \sin \alpha_{\rm T} - b \dot{\psi}}{ v_{\rm T} \cos \alpha_{\rm T}} \right) \\\end{split}\]

Thus, the linearized model can be written as

\[\begin{split}\dot{x} &= v_{\rm T} \\ \dot{y} &= v_{{\rm T},0} \left( \psi + \alpha_{{\rm T}}\right) \\ \dot{\psi} &= \dot{\psi} \\ \dot{v}_{\rm T} &= 0 \\ \dot{\alpha}_{\rm T} &= \frac{F_{y,{\rm F}} + F_{y,{\rm R}}}{m_{T} v_{{\rm T},0}} - \dot{\psi} \\ \ddot{\psi} &= \frac{a F_{y,{\rm F}} - b F_{y,{\rm R}}}{I_{T}} \\\end{split}\]

Neglecting equations of \(x\) and \(v_T\), using the linear tire model (Linear) and writting the state equation in the matrix form we have

(1)\[\begin{split}\left[ \begin{array}{c} \dot{y} \\ \dot{\psi} \\ \dot{\alpha}_T \\ \ddot{\psi} \end{array} \right] = \left[ \begin{array}{cccc} 0 & v_{T,0} & v_{T,0} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & -\frac{K_F+K_R}{m_T v_{T,0}} & - \frac{m_T v_{T,0} + \frac{a K_F - b K_R}{v_{T,0}}}{m_T v_{T,0}} \\ 0 & 0 & - \frac{a K_F - b K_R}{I_T} & - \frac{a^2 K_F + b^2 K_R}{I_T v_{T,0}} \end{array} \right] \left[ \begin{array}{c} y \\ \psi \\ \alpha_T \\ \dot{\psi} \end{array} \right] + \left[ \begin{array}{c} 0 \\ 0 \\ \frac{K_F}{m_T v_{T,0}} \\ \frac{a K_F}{I_T} \end{array} \right] \delta\end{split}\]

Finally, the linearized slip angles are

\[\begin{split}\alpha_{{\rm F},lin} &= \alpha_{{\rm T}} + \frac{a}{v_{{\rm T},0}} \dot{\psi} - \delta \\ \alpha_{{\rm F},lin} &= \alpha_{{\rm T}} - \frac{b}{v_{{\rm T},0}} \dot{\psi} \\\end{split}\]

The cornering stiffness of the chosen tire model for small values of slip angles is calculated as

muy0 = TirePac.a1 * Fz/1000 + TirePac.a2;
D = muy0 * Fz/1000;
BCD = TirePac.a3 * sin(2 * atan(Fz/1000/TirePac.a4))*(1-TirePac.a5 * abs(camber));

Ktire = BCD * 180/pi;

So, the parameters of equation (1) used for the design of the controller are

mT = 1300;
IT = 10000;
a = 1.6154;
b = 1.8846;
vT0 = 16.7;
KF = Ktire;
KR = Ktire;

The linear state space system (Equation (1)) is defined as

A = [      0   vT0            vT0                         0                       ;...
           0    0              0                          1                       ;...
           0    0      -(KF+KR)/(mT*vT0)  -(mT*vT0+(a*KF-b*KR)/(vT0))/(mT*vT0)    ;...
           0    0      -(a*KF-b*KR)/IT    -(a^2*KF+b^2*KR)/(IT*vT0)               ];

B = [   0                  ;...
        0                  ;...
        KF/(mT*vT0)        ;...
        a*KF/IT            ];


C = [1 0 0 0];

The design of the LQR controller can now be done.

Todo

Add illustration of the closed loop system.

The control law is given by

\[\delta = - {\bf K} {\bf z} + K_1 r\]

The double Lane change maneuver is achieved with a step reference point in the lateral position \(y\). Reference become \(r = 2 m\).

The maximum value of the steering angle is limited, i.e., the control input can be saturated.

\[\delta_{max} = \pm 70 deg\]

The weight matrices for the LQR design are

Q = [   3 0 0 0 ;...
        0 1 0 0 ;...
        0 0 1 0 ;...
        0 0 0 1 ];

R = 1;

The control gains are calculated using the lqr function.

Klqr = lqr(A,B,Q,R);

The control law of the lateral dynamics is implemented in the code below.

function controlEffort = ControlLaw(sysData,~)
    % sysData are the informations of the system necessary to generate the control effort
    % controlEffort is the control input of the system

    % In this case, the sysData contains the simple vehicle state variables
    x = [sysData(2);sysData(3);sysData(5);sysData(6)];

    % Vehicle longitudinal position
    X = sysData(1);

    % Lateral displacement
    LateralDisp = 3.6;

    % Reference signal (Double lane change)
    if X <= 15
        r = 0;
    end
    if X > 15 && X <= 70
        r = LateralDisp;
    end
    if X > 70
        r = 0;
    end

    % Control gains
    K = [0.7936    6.6882    1.6107    0.5090];
    u = - K*x + K(1)*r;

    % Saturation of the control effort
    if abs(u) < 42*pi/180
        controlEffort = u;
    else
        controlEffort = sign(u)*42*pi/180;
    end